AC Voltage Calculator
Enter any known quantity to convert between AC voltage values, the form will auto-update as you type.
Block ads by default when you upgrade.
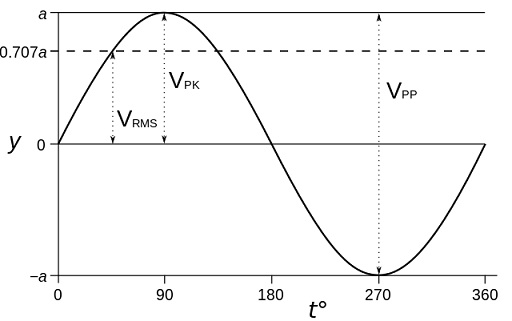
AC Voltage Terms
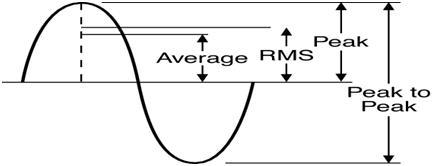
  • Peak Voltage (VPK) The maximum instantaneous value of a function as measured from the zero-volt level. For the waveform shown above, the peak amplitude and peak value are the same, since the average value of the function is zero volts.
  • Peak-to-Peak Voltage (VPP) The full voltage between positive and negative peaks of the waveform; that is, the sum of the magnitude of the positive and negative peaks.
  • RMS Voltage (Vrms) The root-mean-square or effective value of a waveform, equivalent to a DC voltage that would provide the same amount of heat generation in a resistor as the AC voltage would if applied to that same resistor.
  • Average Voltage (Vavg) The level of a waveform defined by the condition that the area enclosed by the curve above this level is exactly equal to the area enclosed by the curve below this level.
Notes
  • RMS is not an "Average" voltage, and its mathematical relationship to peak voltage varies depending on the type of waveform.
  • The RMS value is the square root of the mean (average) value of the squared function of the instantaneous values.
  • Since an AC voltage rises and falls with time, it takes more AC voltage to produce a given RMS voltage than it would for DC. For example, it would take 169 volts peak AC to achieve 120 volts RMS (.707 x169).
  • Most multi-meters, either voltmeters or ammeters, measure RMS value assuming a pure sinusoidal waveform.
AC Voltage Formulas
  • Peak Voltage
  • VPK = 0.5 x VPP
  • VPK = 1.414 x Vrms
  • VPK = 1.571 x Vavg
  • Peak-to-Peak Voltage
  • VPP = 2 x VPK
  • VPP = 2.828 x Vrms
  • VPP = 3.141 x Vavg
  • RMS Voltage
  • Vrms = 0.707 x VPK
  • Vrms = 0.353 x VPP
  • Vrms = 1.111 x Vavg
  • Average Voltage
  • Vavg = 0.637 x VPK
AC Sine Wave
AC Sine Wave Peak vs. Average vs. RMS Voltage
Alternating Current Voltage Sine Wave
Common Conversions
  • RMS Voltage to Peak Voltage
  • RMS Voltage to Peak-to-Peak Voltage
  • RMS Voltage to Average Voltage
  • Peak Voltage to Peak-to-Peak Voltage
  • Peak Voltage to Average Voltage
  • Average Voltage to Peak-to-Peak Voltage

🌐 Connect with like-minded professionals in the electrical testing industry. Our knowledge sharing hub offers a supportive community where you can exchange insights, learn from real-world experiences, and stay at the forefront of electrical testing practices. Join us and expand your expertise!